Batch 3 - Class 221 - Pascal Triangle

• (Moscow - 174) Wheels A,B,C and D are connected with belts as shown. If wheel A starts to rotate clockwise, can all the 4 wheels rotate? In which direction would each wheel rotate?
• 

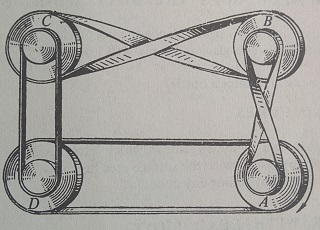  Can the wheels rotate if all 4 belts are crossed?

  Answer: Yes

  What is belt 1 and 3 are crossed?

• Suppose we write down all 10 bit strings. How many 10 bit strings have exactly 4 zeros?
• Each place can be zero or one. Lets work with smaller numbers and start to tabulate the results
• See if kids recall nCk - if not, explain briefly
• Start with n=0,1,2,3,4,5 and different values of k and start to draw the triangle

• What are the interesting observations?
• Symmetric - why? nCk=nC(n-k)? Think in terms of placing zeros in a bit string
• What is the sum of entries in each row? 2^n. Why?
• Each number is sum of two "adjacent" numbers in previous row. Why? nCk=(n-1)Ck + (n-1)C(k-1)
• Lets draw this slightly differently and see more patterns

• Lets look at the pattern along an edge
• First edge 1,1,1,1,1
• Second edge 1,2,3,4,5,6 (counting numbers)
• Third edge 1,3,6,10... - what are these? Triangular numbers (illustrate)
• What do successive triangular numbers total to? Can you think why?
• Fourth edge 1,4,10,20,35... - what are these? Tetrahedral numbers (illustrate)
• Fifth edge 1,5,15,35,70... - can you guess what might these be? Yes, pentatope numbers - number of vertices in a 4-D "triangle"
• Hockey Stick Pattern - Example 1+3+6+10+15 = 35 - Why?
• Parallelogram Pattern - Example - the whole block from left top to 21, totals to 84 - Why? Successive Hockey sticks!
• Lets try one more way of drawing it

• What are the diagonal totals? Does anyone recognize these numbers? Can you think why?
• Can you spot them on the original Pascal triangle?
• There are several other advanced patterns hidden in Pascal triangle - such as value of e, pi, star of david, catalan numbers...

• (Geoffrey - 161 Modified) The sketch below shows the plan of industrial establishment with secret weapons. There are only three gates which are guarded. There is some information leakage, and they found this note supposedly written for the spy

• Answer: this is same as ways of arranging a number of 1's in a bit string. Since 210 appears as 5th number in 11th row, it must be at intersection of 7th and 5th Street (there is only one such combination above - if it was a larger grid, there would be two possibilities)